Basic Principles of Problem Solving

IMPORTANT NOTE: IF ANY OF THE SYMBOLS OR TERMINOLOGY ON THIS PAGE CONFUSES YOU, PLEASE HIT THE BUTTON BELOW AND READ "Conventions and Symbols" BEFORE RETURNING TO "Basic Principles of Problem Solving."

When attacking a physics problem the first thing to remember is you CAN solve it. If it wasn't solvable, it wouldn't have been assigned. Some problems are more difficult than others, but all can be solved and furthermore, you have the capability to do it. Also, physics problems just LOOK difficult. Don't let the wording of the problem scare you. We will begin by applying the basic principles to a simple kinematics problem. But do remember that these can apply to ANY problem.

Alice drops a baseball straight down from the top of a 200-meter tall building. Ignoring air resistance and assuming that its a bright, sunny, calm and clear day, what is the velocity of the ball right before it hits the ground? The acceleration due to gravity is 9.8 m/s²

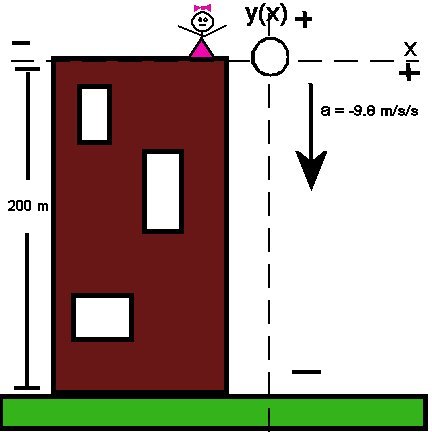
1. Draw a picture. This frees up valuable memory space and mental power than can be applied to solving the problem - instead of just remembering what it is. The drawing should be neat and legible, so that YOU understand it.. Don't worry if its not "pretty." This is not an art assignment and you are not Michelangelo. Label the picture and be sure to put in a frame of reference. Placing a frame of reference in your drawing means assigning a point at which the problem starts (time = 0, velocity = 0, etc). This is done by assigning a coordinate axis. For simplicity, place the beginning of the problem at the origin. The cool thing is that the orientation of the axis is entirely up to you. If you want the "down" direction to be positive, then it can be positive, making the "up" direction negative. Whatever works for you. I have chosen the down direction to be negative, which means that all activities in that direction be assigned a negative value.

Alice drops a ball straight down from the top of a 200-meter tall building. Ignoring air resistance and assuming that its a bright, sunny, calm and clear day, what is the velocity of the ball right before it hits the ground? The acceleration due to gravity is 9.8 m/s²

Please note that my picture looks more like a Picasso than something by a great classical master. Like I said, not an art assignment. But also note that the drawing has all the information we need to set up the equations to solve the problem. I have chosen to make the down direction negative, as is traditional. Feel free to draw your own picture and assign your reference frames as you want them to be. Also note that this is not to scale. Alice is several stories high and the ball is almost bigger than she is. Tough Cookies.. The picture tells you what you need to know.

2. Write down what information you have (don't forget to assign the appropriate sign to your information), and what information you need. It is vital that you understand what you are looking for when you try to solve a problem. If you don't know what you're looking for, you won't know when you get there. Remember, be organized. Once again, this should be neat and legible. Learn to filter the good, relevant information from the irrelevant information. It doesn't matter if Alice is dropping the ball or if Bob is dropping the ball. It doesn't matter if is an apartment building or a skyscraper. It doesn't matter if the ball is being dropped off the roof or from an office window, or what the weather is. You don't need to take air conditions into account unless expressly told to, and since this complicates the problem exponentially, I doubt you'll be encountering that at this stage in your physics career. If you are doing physics that advanced, I'm sorry to inform you that I just haven't had the time to expand this website that far.

In this case, the question is "what is the velocity of the ball right before it hits the ground?" so we are looking to solve for final velocity.

3. Figure out what information is inferred...that is, what is implied but not expressly given? It very important to recognize the existence of this information! In our example of Alice and the Baseball, the initial velocity is not stated. However, since Alice is standing on the edge of a building and is not moving, we can assume that when she drops the ball, it begins to fall from a state of rest. Initial Velocity is therefore inferred to be equal to 0 m/s.

4. Determine what formula(s) applies to the problem. What formula you use will depend on what information you have and what information you are looking for. Ideally, the formula you choose will allow you to solve for the missing piece of information as the only unknown. Write the formula down. Sometimes more than one formula will apply. In the case of Kinematics, there are six formulas to choose from. Write them all down! The more options you have, the better. Just make sure that they are applicable to the problem. You don't want to write electromagnetic equations down for a conservation of energy problem. Also, writing down the equations at the beginning of every problem will help you memorize them. This is an added bonus as you may not be permitted to use the formula sheet on the test. So, we will write down the kinematic equations and see if any of them can be used to help us solve our little time dilemma.

All of these are very nice, helpful, friendly formulas, but we only need one to solve the problem. The formula we are looking for allows us to input the information we have while only leaving us with one unknown. This will permit us to solve for the unknown (in this case, final velocity) and then we will have our answer. We KNOW the values for s, s_o, a, and v_o. So, we select equation #5 to help us solve our problem. Imagine, if you will, that this makes Equation #5 very happy, but do not feel guilty at all for discarding the other five equations. You will use them in other problems.

5. Solve the equation for the unknown variable before you plug in the information you have. Doing all the algebraic manipulations first will simplify the problem-solving process. In this case, there only manipulation required is to take the square root of each side. Then plug your information in and calculate the unknown! Tip: Make sure all your units cancel appropriately.

6. Now use common sense to check your answer. Is it reasonable? Yes, 62 m/s is reasonable. This is a very fast velocity, but remember that Alice dropped the ball from a 200 m building. If every story is approximately 15 feet, this is a 44 story office building. The farther the ball goes, the faster it will fall. Alice should be very grateful that the ball didn't hit anyone on the way down. Are the units of your answer appropriate to the unknown you were solving for? Yes, the units are exactly what we would expect them to be. The units of velocity are m/s and that is the result we got when we calculated the final velocity.

You will find that many of the problems you encounter have multiple parts. All the above steps still apply to each part of the problem. However, it is not necessary to calculate everything a second time to ensure accuracy. Instead you can transmute the information you calculated in the first part to any remaining parts. Modification may be required, but these are simple in nature. See Average Velocity & Speed for an example.

Sometimes solving a problem will require extra steps...don't panic! The formula outlined on this page is just the basics. Each problem solved in Solve-It Physics will make note of the extra steps required. Just look up that specific type of problem for more details.

These basic steps will apply to all physics problems. Some problems are more complicated then others and require more innovation and manipulation but you are now prepared to tackle your homework!